Intersección
Requiere formar un nuevo conjunto con los elementos comunes de los conjuntos dados.
Ejemplo :

Diferencia
Formar un nuevo conjunto con los elementos diferentes del primero de ellos.
Ejemplo :

Diferencia Simétrica
Formar un nuevo conjunto con los elementos diferentes de los dos conjuntos dados.
Ejemplo :

Producto Cartesiano
Resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse tomando el primer elemento del par del primer conjunto, y el segundo del segundo conjunto.
Ejemplo :
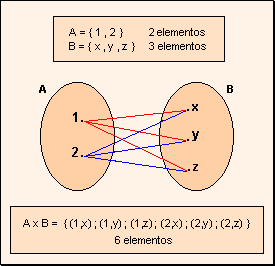
Además de ver las operaciones de conjuntos, vimos un tema llamado Cardinal de la Unión y Cardinal de un producto cartesiano
Cardinal de la Unión
Suma de los cardinales de los conjuntos, menos el cardinal de la intersección.
n(AuB) = n(A) + n(B) - n(A int. B)
Encuentre n(A) si n(AuB) = 75, n(B) = 50, n(Aint. B)= 30
75 = n(A) + 50 - 30
75 - 50 + 30 = n(A)
55 = n(A)
Cardinal de un Producto cartesiano
si n(A)= a y n(B)= b, entonces n(AxB) = n(BxA) = n(A) x n(B) = n(B) x n(A) = ab
Encuentre n(AxB) y n(BxA) si
A = {a,b,c,d,e,f,g} y B = {2,4,6}
n(AxB) = 7 x 3 = 21
Además, la ingeniera nos puso a trabajar una hoja en nuestro cuaderno de ejercicios, y ahí fue donde vi que los temas de las operaciones de conjuntos combinadas me cuestan un poco.
A mi parecer, las operaciones de los conjuntos me son sencillas a la hora de hacerlos individualmente, pero siento que cuando se combinan ciertas operaciones una o más de una vez, me confundo mucho y me cuesta saber qué operación es cada cuál. Se podría decir que esa es mi única dificultad en todos los temas que vimos el día de hoy.
Tamién, trabajamos el reto # 19 en clase, decía así:
El contador de kilómetros de mi carro muestra 72,927 , que es un número capicúa (se lee igual empezando por el final). ¿Cuántos kilómetros debo recorrer como mínimo para poder ver otro número capicúa en mi contador de kilómetros?
No hay comentarios:
Publicar un comentario