El día de hoy terminamos de ver lo que son todas las operaciones con conjuntos.
Intersección
Requiere formar un nuevo conjunto con los elementos comunes de los conjuntos dados.
Ejemplo :
Diferencia
Formar un nuevo conjunto con los elementos diferentes del primero de ellos.
Ejemplo :
Diferencia Simétrica
Formar un nuevo conjunto con los elementos diferentes de los dos conjuntos dados.
Ejemplo :
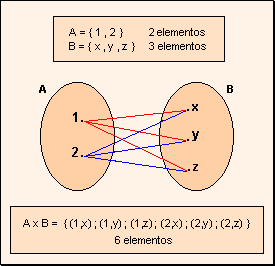
Producto Cartesiano
Resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse tomando el primer elemento del par del primer conjunto, y el segundo del segundo conjunto.
Ejemplo :
Además de ver las operaciones de conjuntos, vimos un tema llamado Cardinal de la Unión y Cardinal de un producto cartesiano
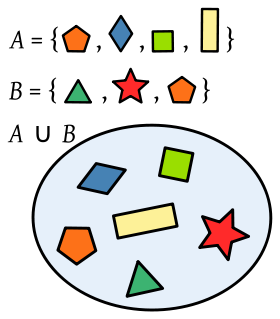
Cardinal de la Unión
Suma de los cardinales de los conjuntos, menos el cardinal de la intersección.
n(AuB) = n(A) + n(B) - n(A int. B)
Encuentre n(A) si n(AuB) = 75, n(B) = 50, n(Aint. B)= 30
75 = n(A) + 50 - 30
75 - 50 + 30 = n(A)
55 = n(A)
Cardinal de un Producto cartesiano
si n(A)= a y n(B)= b, entonces n(AxB) = n(BxA) = n(A) x n(B) = n(B) x n(A) = ab
Encuentre n(AxB) y n(BxA) si
A = {a,b,c,d,e,f,g} y B = {2,4,6}
n(AxB) = 7 x 3 = 21
Además, la ingeniera nos puso a trabajar una hoja en nuestro cuaderno de ejercicios, y ahí fue donde vi que los temas de las operaciones de conjuntos combinadas me cuestan un poco.
A mi parecer, las operaciones de los conjuntos me son sencillas a la hora de hacerlos individualmente, pero siento que cuando se combinan ciertas operaciones una o más de una vez, me confundo mucho y me cuesta saber qué operación es cada cuál. Se podría decir que esa es mi única dificultad en todos los temas que vimos el día de hoy.
Tamién, trabajamos el reto # 19 en clase, decía así:
El contador de kilómetros de mi carro muestra 72,927 , que es un número capicúa (se lee igual empezando por el final). ¿Cuántos kilómetros debo recorrer como mínimo para poder ver otro número capicúa en mi contador de kilómetros?